01. Realizing Half and Full Adders

Owner	MM. G. Sadek
Tags

01 - The Objective

In this tutorial, we will learn how to design and implement half and full adders using different logic gates. The theory is simple, Binary addition is similar to that of decimal addition. Add the first digits of a number and if the count exceeds binary 2, then carry ‘1’ to the next row.

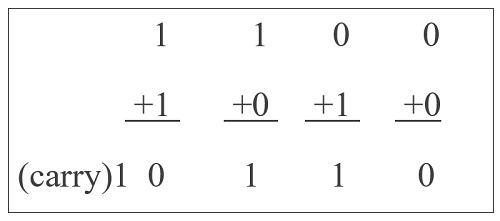
02 - The Design

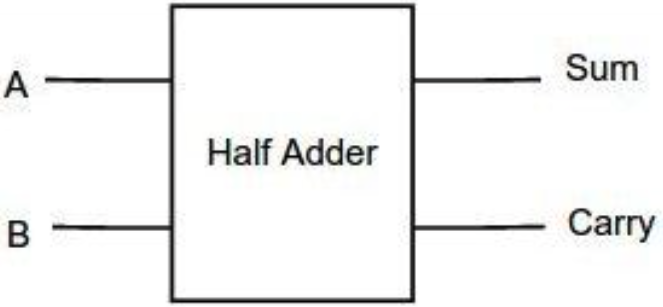
02.A. The Half Adders

In order to design any combinational logic circuit, we need to write down its truth table. In our case, we will design a half adder that adds two bits together and outputs a sum value and a carry value.

Input		Output
A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	1	1

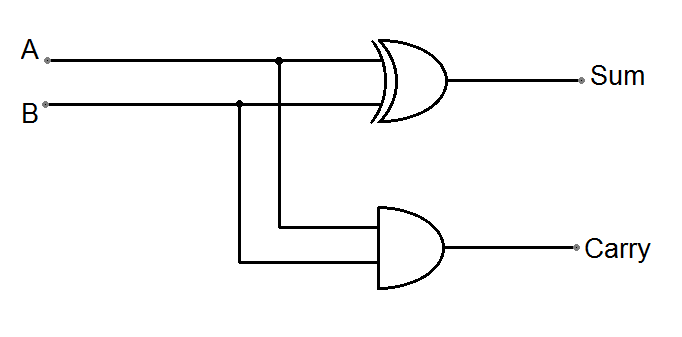
If you observe the truth table, the sum output of the binary addition carried out above is similar to that of an Ex-OR operation, while the carry output is similar to that of an AND operation. Therefore, the half adder can be implemented using XOR and AND gates.

02.B. The Full Adder

This is halfway through when implementing an adding circuit since in any binary adding operation we need to consider the carry-in from the previous bitwise addition. Therefore, the full adder extends the half adder to include a carry-in bit. So we need to extend our truth table to include this bit:

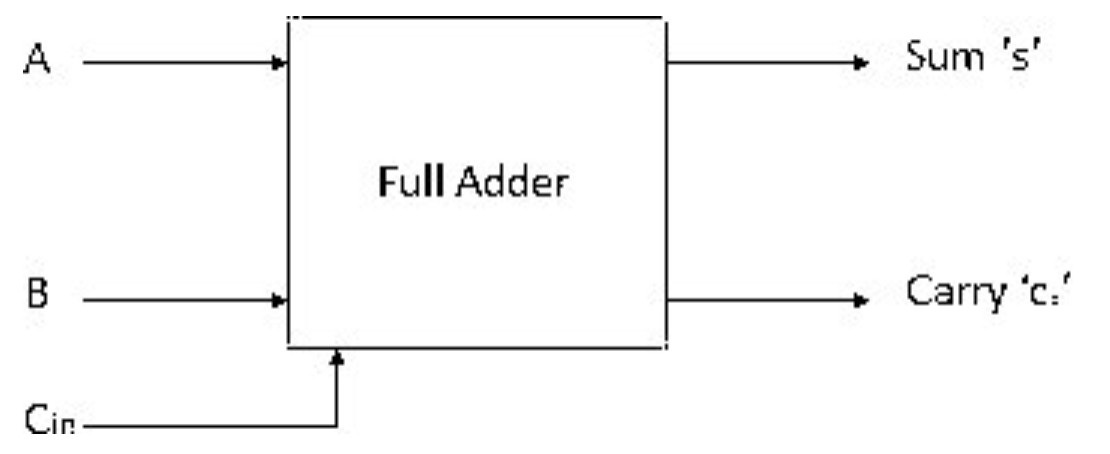
From the truth table, we can express the sum and carry using:

sum=\bar{A}.\bar{B}.C_{in}+\bar{A}.B.\bar{C_{in}}+A.\bar{B}.\bar{C_{in}}+A.B.C_{in}

c=A.B+A.C_{in}+B.C_{in}

Input			Output
Carry-in	A	B	Sum	Carry
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	1	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

At this point you can realize the full adder in two ways:

02.B.I. Traditional way

You can realize the sum and carry boolean functions as shown:

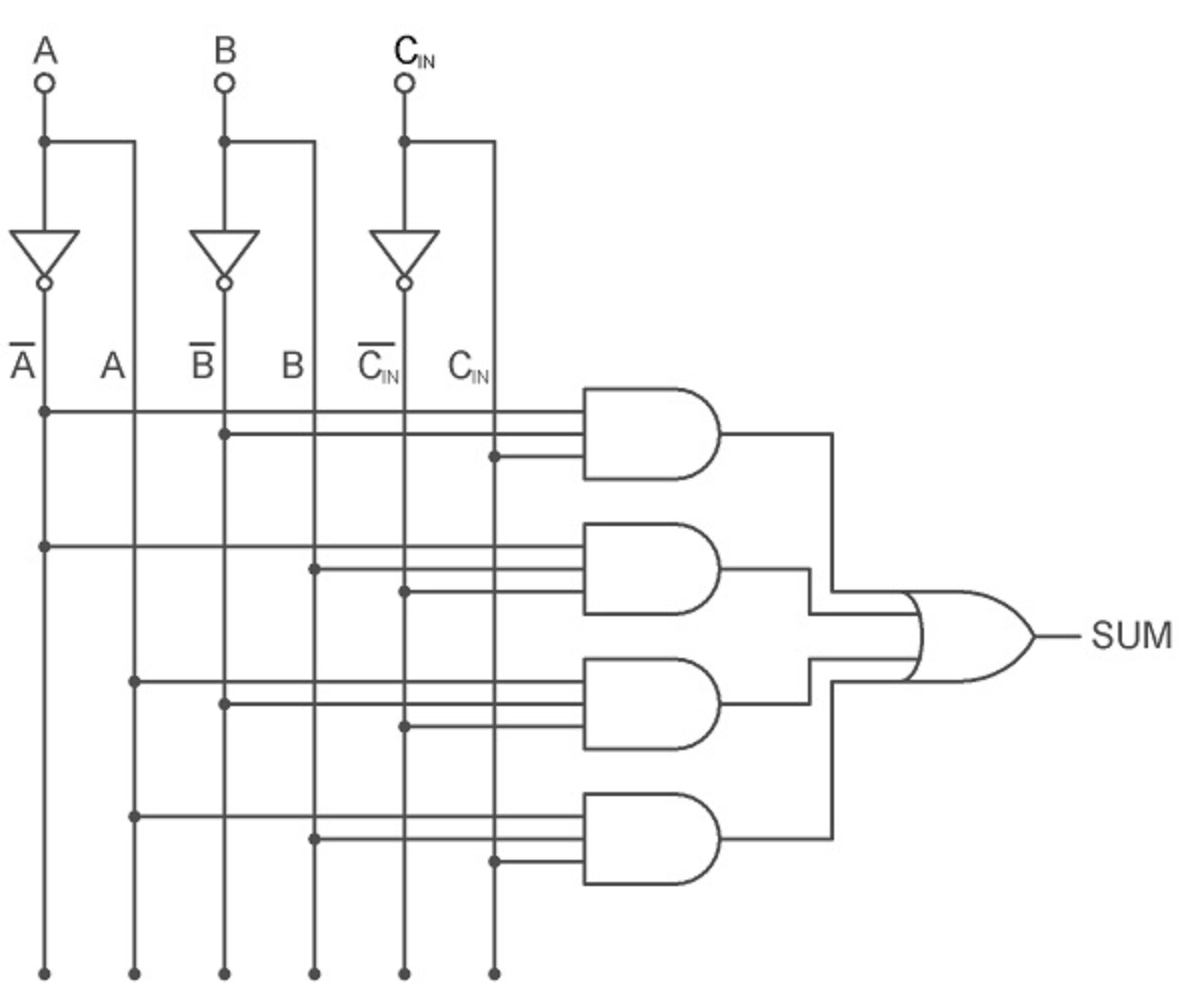
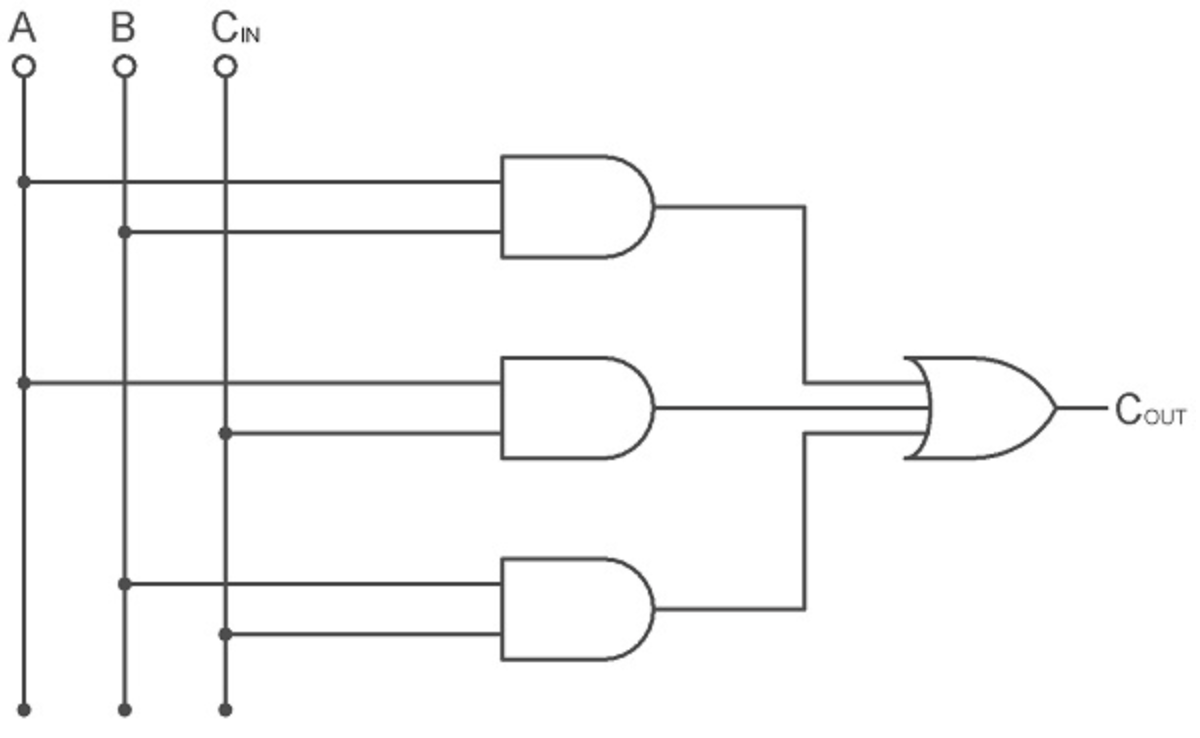
02.B.II. Using half adders

On the other hand, you can cascade two half adders to have a 1-bit full adder as shown:

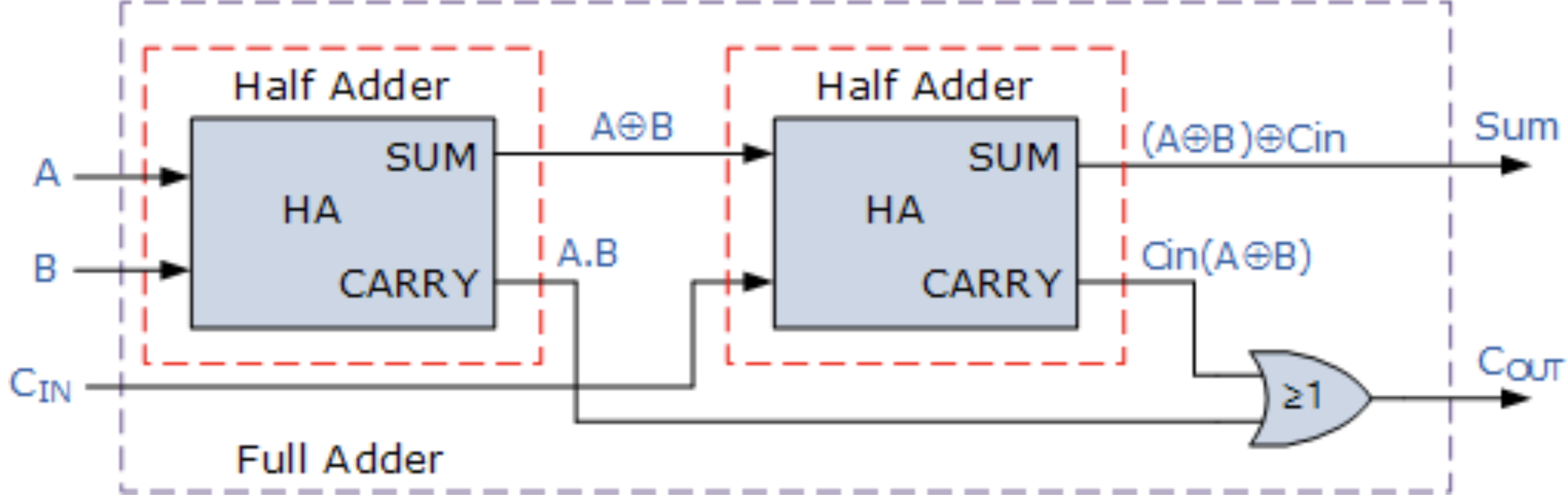
03. Classwork

In this tutorial, we are asking you to :

Implement a 2-bit full adder using half-adders.

Use the full adder IC to verify your connection.